The following article is reprinted with permission from Orvin E. Wagner, "A Plants Response to Microgravity as a Wave Phenomenon", AIP Conference Proceedings 504, 2000, pp. 368-373. ©2000, American Institute of Physics. This article may be downloaded for personal use only. Any other use requires prior permission of the author and the American Institute of Physics. Dr. Wagner gave the invited presentation on February 2, 2000, in Albuquerque. Click here to visit the American Institute of Physics' Conference Proceedings.

A Plant's Response to Microgravity as a Wave Phenomenon

Orvin E. Wagner

Wagner Research Laboratory, Grants Pass, OR 97527

Telephone: (541)507-1539; E-mail: oedphd@gmail.com

ABSTRACT

Simple observations of plants growing on earth indicate that plants are operated by heretofore unknown waves that interact strongly with gravity. Indications of these waves and their interactions with earth's gravity include discrete frequencies derived from internodal spacings, discrete preferred angles of growth for branches, ratios of averages of reciprocals of horizontal and vertical internodal spacings that are ratios of small integers, and linear relationships between angles of growth and means of reciprocals of cell lengths. It is proposed that the lengths of cells grown in a microgravity environment be studied to see if the mean frequencies derived from cell lengths are uniform in every direction and match frequencies derived from cells grown horizontally on earth. If this is the case, then apparently no orientation dependence exists. Thus all directions would be completely equivalent to a plant growing in a microgravity environment. The cell parameters obtained would then indicate that centripetal force and gravity are equivalent for plants grown in a microgravity environment. Also one could find out if a plant's ability to function in space is improved if the plant being tested has a minimum sensitivity to gravity on earth.

INTRODUCTION

In 1988 I discovered low velocity longitudinal waves in plants and subsequently studied their basic characteristics (Wagner, 1988-1999). These waves are called W-waves because they were first found by probing freshly cut live wood. The initial velocity found for these waves was found to be close to 1 m/s (Wagner, 1989,1990). These waves don't appear to be explicitly electromagnetic but in live materials they shift charge because charge is free to move. These waves usually appear as standing waves so that with multiple probes or probing one can often find evidence for a standing waves in plant materials with charge located in periodically spaced piles. Standing waves appear to be responsible for the placement of structures such as branches or leaves (Wagner, 1990 and subsequent papers). The standing waves also appear to have an important influence on determining the size and shape of cells and shorter wavelengths are hypothesized to be important in determining cell structure (Wagner 1999). The author is of the opinion that W-waves are really an extension of quantum waves to the macroscopic with a continuous connection to the microscopic. The waves are also found outside of plants traveling with much larger velocities (v). W-waves appear to have many unique frequencies (f). These frequencies can be measured electronically, by beating with weak electromagnetic signals (Wagner 1989, 1990) and directly with a low frequency spectrum analyzer. One can also measure plant internodal spacings (s) and use these measurements to calculate the same characteristic plant frequencies using a previously measured wave velocity (Wagner, 1990, 1996). A frequency for a particular spacing is given by f=v/2s since we assume an internodal spacing is determined by a half wavelength of a standing wave. Characteristic plant frequencies repeat from plant to plant.

For this paper the most important observation is that W- waves seem to be influenced tremendously by the gravitational field in the structure of the plant. The amount of influence seems to be dependent on the plant structure. The velocity of these waves within a plant may be different depending on whether they are traveling along the gravitational field or perpendicular to it or at angles in between (Wagner, 1996, 1997). The frequencies of the waves may also be shifted to lower values when traveling along the gravitational field as compared to traveling perpendicular to the gravitational field (Wagner 1996) (Figures 1 & 2).

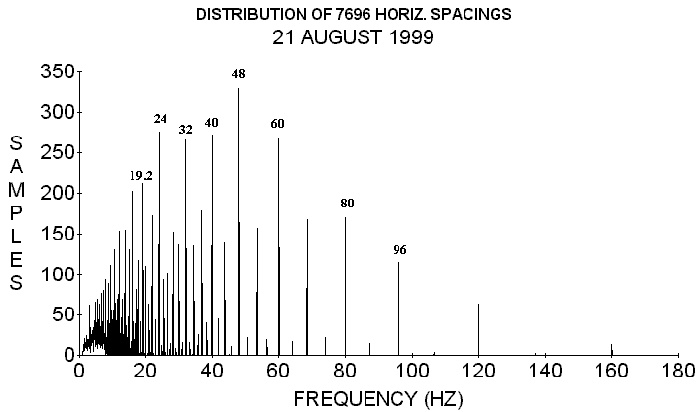
FIGURE 1. Using 96 cm/s for the velocity this is a distribution of internodal spacing frequencies derived from 7696 horizontal internodal spacings on plants. Compare the major peaks with those of Figure 2. Notice that the frequencies here are considerably larger on average. (From O. E. Wagner, Physiol. Chem. Phys. &; Med. NMR 28, 173-196 (1996). Used by permission)

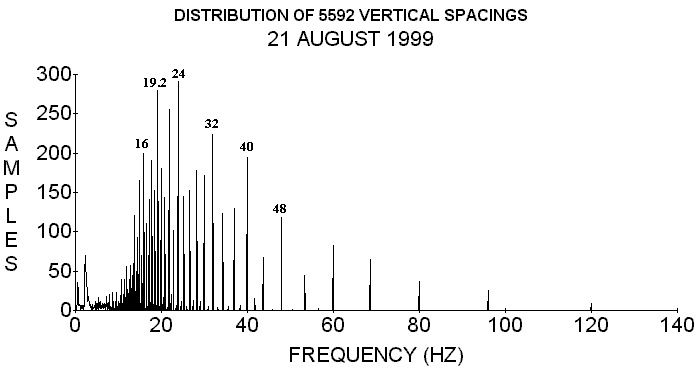
FIGURE 2. Again using 96 cm/s for the velocity this is the internodal spacing frequency distribution of 5596 vertical internodal spacings. Notice how the apparent frequencies are in general lower than those in Figure 1. (From O. E. Wagner, Physiol. Chem. Phys. & Med. NMR 28, 173-196 (1996). Used by permission)

The species from which the spacings were taken, using a linear measuring instrument, in Figures 1 and 2 are Red alder (Alnus rubra), delicious apple (Pyrus Malus sp.), Himalaya blackberry (Rubus thyranthus), bracken fern (Pteridium equilinium), golden chinkapin (Castinopis chrysophylla), weeping flowering cherry (Prunus subhintella), Douglas fir (Pseudotsuga menziesii), false indigo (Amorpha fruiticosa), big leaf maple (Acer macrophyllum), Grand fir (Abies grandis), ponderosa pine (Pinus ponderosa), weeping birch (Betula pendula), Hind's willow (Salix hindsiana), golden weeping willow (Salix sp.), Dutch elm (Ulmus hollandica), and sweet corn (Zea mays sacarata). Most of these plants grew in the vicinity of the laboratory. Since spacings appear to repeat from plant to plant these graphs should include most plant frequencies except some of those with very short or very long internodal spacings.

In the wave model gravity may shift mean apparent frequencies to one third of the horizontal (or maybe even to a smaller fraction) in live plant material. This results in mean cell lengths and internodal spacings being up to three (or even more) times longer parallel to the gravitational field compared to perpendicular to the gravitational field. Thus if the gravitational field is missing or nearly so as with the microgravity the cell is missing the reference that determines its shape, for example (Halstead and Dutcher, 1987). It also appears that plant parts grow at discrete angles to the gravitational field as discussed in the next section.

PLANT GROWTH AT VARIOUS ANGLES TO THE GRAVITATIONAL

For several years I observed that often certain portions of branches of plants seemed to grow straight for considerable distances. In one case I found a red alder branch that grew away from the trunk for almost three meters with every portion of the branch including secondary branches almost perfectly level. In 1997 I published a paper describing the results of several hundred measurements of angles that these straight portions of branches made with the horizontal (Wagner, 1997). I found that branches seem to preferentially grow at approximately integral multiples of five degrees with the horizontal. The following graph is the result of combining all the angle data from the article plus a few more (948 total angles). The data were taken with a smart level in late June and early July (1996) when the branches were fully loaded with leaves and apparently equilibrium had been attained. Instead of drooping, forces seem to keep the branches growing straight for considerable distances. In the given cases the straight growth was for at least one half meter. 82 % of the angles of the straight portions were found to have grown within one degree of integral multiples of five degrees as the following graph demonstrates.

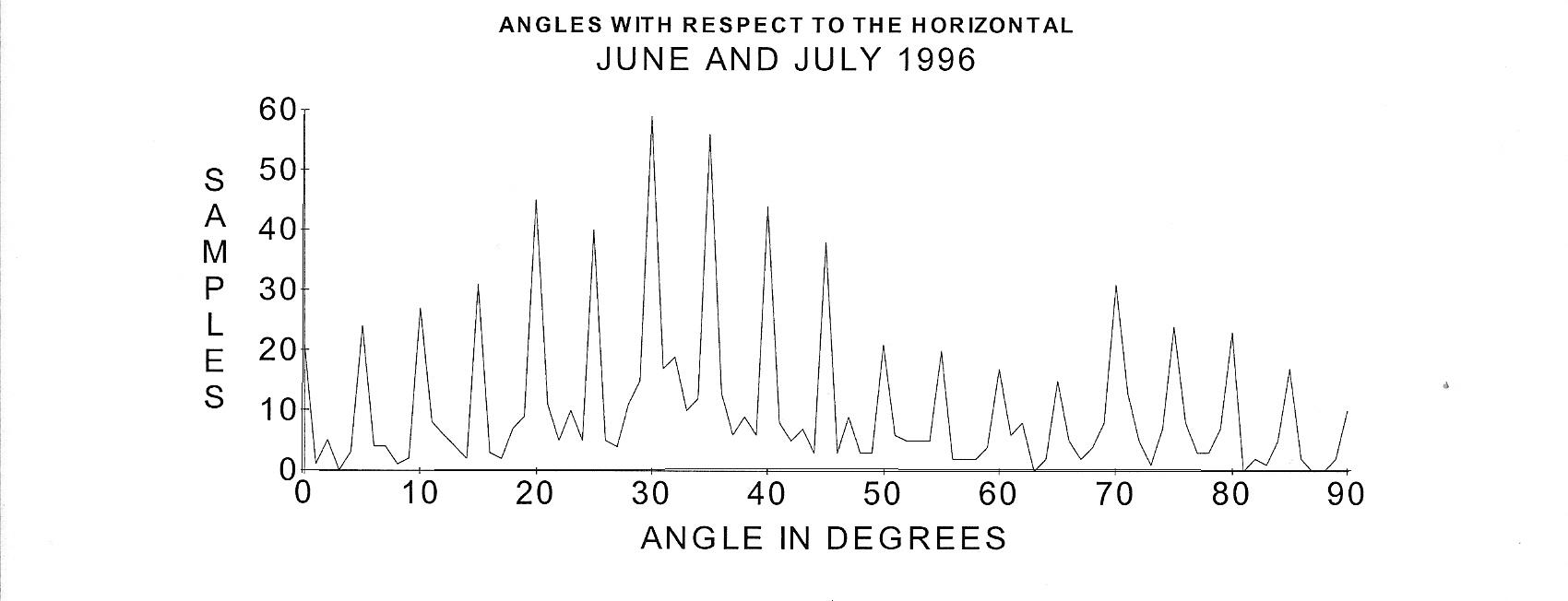
FIGURE 3. A distribution of 948 angles of straight growth measured with respect to the horizontal from several species of trees. The distribution indicates that the angles of growth appear to be predominantly near integral multiples of near 5 degrees. The data were taken from red alder (Alnus rubra), big leaf maple (Acer macrophylla), Douglas fir (Pseudotsuga menziesii), golden weeping willow (Salix sp.), hazelnut (Corylus sp.), ponderosa pine (Pinus ponderosa), and an unidentified tree species. (From O. E. Wagner,Physiol. Chem. Phys. & Med. NMR 29, 63-69 (1997). Used by permission)

The kind of behavior observed suggests strongly that the waves involved are interacting with gravity in a quantum like manner. The author was aware that he could bias the measurements so he went out of his way to be sure the data were correct by checking with a digital "smart level" that could be read to better than one half of a degree. Care was also taken to assure that branch roughness did not bias the measurements. This observation of the five degree increments with respect to gravity suggests that there are standards to correct to so that uniformity is achieved in growing plants.

INTERNODAL SPACING AND CELL GROWTH AT DIFFERENT ANGLES TO THE GRAVITATIONAL FIELD ON EARTH

For several years I studied the ratios of mean frequencies of internodal spacings (distances between structures on plants such as the distances between leaves and branches). One problem was that it is difficult to find and measure many internodal spacings that grow at angles other than vertical and horizontal. Some of the results from the horizontal and vertical internodal spacing data are shown in Table 1. Here I took reciprocals of spacings multiplied by two and then multiplied by 96 cm/s. I then found the means of the different sets of reciprocal ratio data. 96 cm/s was used as the W-wave velocity because it was the most commonly measured velocity in the early work. A constant velocity was assumed for comparison purposes even though different velocities may be present at different angles to the gravitational field.

TABLE 1. Horizontal/vertical Internodal Frequency Ratios

Species	Number of spacings	Reciprocal ratio (H/V)	Possible velocity Ratios
Big Leaf Maple	HORIZ.=205	7.10/4.81=1.48	3/2
	VERT.=122
Golden Weeping Willow	HORIZ.=760	27.99/19.83=1.66	5/3
	VERT.=685
False Indigo	HORIZ.=361	39.34/29.54=1.33	4/3
	VERT.=376
Delicious apple	HORIZ.=618	29.99/21.68=1.33	4/3
	VERT.=636
Weeping Birch	HORIZ.=380	28.35/22.71=1.25	5/4
	VERT.=553
Golden chinkapin	HORIZ.=657	45.76/29.32=1.56	3/2
	VERT.=373
Ponderosa Pine	HORIZ.=429	3.25/1.09=2.98	3/1
	VERT.=164
Hind's willow	HORIZ.=429	57.68/39.01=1.48	3/2
	VERT.=164
Red alder	HORIZ.=472	15.93/9.38=1.70	5/3
	VERT.=794

Table 1 shows ratios (H/V) of the means of reciprocals of horizontal and vertical internodal spacings from 9 species of trees and shrubs. The ratios here could be due to differences in velocity between vertical and horizontal or due to difference in frequency averages as was indicated in Table 2 for data taken from lengths of xylem cells. In Wagner 1996 it was assumed that velocity ratios are involved because I directly measured velocities with such ratios but the cell data given in this paper may imply frequency ratios which was a possibility given in Wagner, 1996. It is believed plants can utilize both different velocities and different frequencies in gene implementation of plant structure. (From O. E. Wagner, Physiol. Chem. Phys. Med. NMR 28, 173-196 (1996). Used by permission)

After measuring many internodal spacings, cell lengths from xylem tissue growing at specific angles to the horizontal were measured. Easy cells to measure are wood cells (tracheids, true fibers, and vessel elements) from the xylem of trees. Unlike internodal spacings many samples of cell lengths growing at different angles to the gravitational field are easy to find and analyze using a ordinary optical microscope after simple chemical separation of the xylem cells. I measured thousands of cell lengths (s) grown at different angles to the gravitational field (actually with respect to the horizontal which is the complementary angle). I again converted these reciprocals to frequency (f) using 96 cm/s (v) and then took averages of these frequencies (at least 300 for each vertical or horizontal case) . Table 2 shows the results from surface xylem cells of five different species together with the angles of growth with reference to the horizontal for the specific samplings:

TABLE 2. Mean Frequencies Versus Angle

Species	0°	5°	45°	65°	75°	80°	85°	90°
Oregon ash (Fraxinus latifola)	1110		820		551			431
Pacific madrone (Arbutus menziesii)	1317		1007	877		775
Black cottonwood (Populus trichocarpa)		936	876				829
California black oak (Quercus kellogii)	642		493			420
Incense cedar (Libocedrus deccurens)	503		358					195

Table 2 gives mean frequencies (f=v/2s) derived from cell lengths (from xylem cells) growing at the given angles to the horizontal. One can plot almost a straight line for each species for angle versus mean value. Again the frequency apparently is shifted toward lower values (and/or the velocity is changed accordingly) as the angle approaches 0 degrees with the gravitational field. A linear relationship with angle seems to be found here although it could be that the relationship is linear with the sine of the angle in some cases. It would seem reasonable that the mean of the reciprocals should change linearly with the sine of the angle. The quantum nature of the observed angles (Wagner, 1997) may change the relationship, however to linear with angle rather than with sine of the angle as I would have predicted. The taking of reciprocals seems to be necessary to obtain the linear relationships implying that waves are involved. (From O. E. Wagner, "A Plants Response to Gravity as a Wave Phenomenon", The J. of Grav. Physiol. 6(1) (1999). In Press. Used by permission)

It was also observed but not published that for increasing magnitudes of angle less than zero degrees the frequencies again decrease. For angles between zero and ninety degrees, for the given trees, one can approximately describe the decrease in frequency with the equation f=f0 - kq where f is the frequency, f0 is the frequency at zero degrees, k is the slope of the line given by the difference, the frequency at zero degrees minus the frequency at ninety degrees, divided by 90 degrees, for example.The given equation doesn't take into account quantization of angles. If precise quantization is the case then one can replace the q with 5n with n=0,1,2,3....18. The given k could be called the gravitational sensitivity of the plant. I will, however, define the gravitational sensitivity as simply R=H/V where H is the mean of sample internodal spacing or sample cell length reciprocals and V is similarly the mean of vertical internodal spacing or cell length reciprocals. Note that ratios from spacings and ratios from cells may be somewhat different in the same plant. The possibility that velocities are a large function of frequency could have an influence here and in the finding of apparent multiple velocities (Wagner, 1996).

CELL GROWTH AT DIFFERENT ANGLES TO THE VERTICAL IN THE MICROGRAVITY FIELD

In the microgravity in a spacecraft the gravitational field is essentially canceled because of the centripetal field. This suggests that the only permitted frequencies for growth in microgravity are the ones that pertain to horizontal growth on earth. Also the angular quantization would be expected to be missing. The result is that the plant is constrained to grow uniformly in every direction as far as the gravity and centripetal fields are concerned if the principle of equivalence applies here. It is interesting to observe that the centripetal field and the gravity field, so far, have been considered equivalent to plants for W-waves. This is true with the principle of equivalence but to me this puts the idea of gravity being a curvature of space phenomenon as Einstein assumed in doubt because curvature of space does not seem to explain inertia or momentum. The study of a plants response to gravity may open up new ways of looking at gravity. For example perhaps gravity is a very short wavelength wave phenomenon.

Almost everyone has assumed that plants react to centripetal force and gravity in the same manner (Salisbury 1999). This may not be exactly true so perhaps measurements from plants grown in a microgravity environment would clear up the matter. As an initial experiment we would like to determine if any cell shape anisotropy as a function of orientation can be detected at all in a microgravity environment. One would have to use the proper lighting to prevent growth anisotropy due to lighting. If uniform lighting can be achieved then one can check if any possible difference in effect can be found between centripetal forces and ordinary gravitational forces on earth. One needs to be sure that all the plant interactions that pertain to gravity are known. This may require more measurements. The process requires taking measurements similar to the above for wood and other cells grown in the microgravity field. There likely would not be a large enough sampling of internodal spacings to measure on plants grown in a microgravity environment. Plant cells, however, with their many different orientations should be available in abundance for measurement as long as the particular plant chosen will grow in the microgravity environment. One should probably choose woody plants that are proven to be sensitive to gravity from a large earthly horizontal reciprocal to vertical reciprocal ratio (R). It is my hypothesis that plants with a small R would be more likely to grow well in a microgravity environment, however. This is a hypothesis that could be tested simultaneously in the experiment. In some plants (such as black cottonwood in table 2) the ratio between horizontal reciprocal and vertical reciprocal averages was found to be close to one. All plants so far measured on earth always show at least a small ratio which is greater than one. The results would be related to the principle of equivalence, gravitational theory, and plant-gravity interactions.

CONCLUSIONS AND OBSERVATIONS

The wave approach to a plant's interaction with gravity appears to answer many of the questions about how plants are influenced by the gravity and microgravity fields. With the additional knowledge about how a plant grows and responds to gravity we may be able to alter the environment to produce different types of desired growth. Perhaps one can generate the proper fields to produce an environment that will allow plants to grow as if they were on earth while in a microgravity environment. If the wave theory applies to plants it likely applies in subtle ways to other life. Likely cell growth of all kinds is influenced, to at least some extent, everywhere, by the direction and magnitude of the gravitational field. The subtle influences are likely important to man's survival at any location in space.

REFERENCES

Halstead, T.W. and Dutcher, F.R., "Plants in Space", Ann. Revs. of Plant Physiol. 38, 317-345 (1987).

Salisbury, F. B., "Gravitropism: Changing Ideas", Horticultural Revs. 15, 233-278 (1993).

Salisbury, F. B., Private communication., (1999).

Wagner, O.E., "Acceleration Changes within Living Trees", Physiol. Chem. and Phys. & Med. NMR 27, 31-44 (1994).

Wagner, O.E. , "Acceleration Changes within Plants", Physiol. Chem. and Phys. & Med. NMR 24, 29-33 (1992).

Wagner, O. E., "Anisotropy of Wave Velocities in Plants: Gravitropism", Physiol. Chem. Phys. & Med. NMR 28, 173-196 (1996).

Wagner, O.E.,"Quantization of Plant Growth Angles With Respect to Gravity", Physiol. Chem. Phys. & Med. NMR 29, 63-69 (1997).

Wagner, O.E., "Wave Behavior in Plant Tissue", Northw. Sci. 62, 263-270 (1988).

Wagner, O.E., "Wave Energy Density in Plants", Physiol. Chem. and Phys. & Med. NMR 25, 49-54 (1993).

Wagner, O.E., "Waves in Dark Matter", Physics Essays. In Press (1999).

Wagner, O.E., Waves in Dark Matter, Rogue River, Wagner Physics Publishing, 1995, pp. 1-188.

Wagner, O.E., "W-waves and Plant Communication", Northw. Sci. 63, 119-128 (1989).

Wagner, O.E., "W-waves and Plant Spacings", Northw. Sci. 64, 28-38 (1990).