The following article appeared in the March 1999 issue of Physics Essays. This article presents a valid basis for the idea that the Universe is self organizing which has been recognized by many. This article especially emphasizes how the solar system was formed and how it remains stable. These problems have never really been solved before but this article provides reasonable answers. This paper was submitted to Physics Essays in May 1994. Much of the material in this paper was first published in a book entitled W-Waves and a Wave Universe in 1991. This article posted with permission from Physics Essays. Click here for more about the journal Physics Essays.

ABSTRACT. The hypothesis that longitudinal standing waves in the dark matter-vacuum medium are responsible for placing the planets suggests an equation that describes the location of the orbits of the planets and their satellites. This equation also suggests a wave velocity equation as well as a solution to a wave equation. The equation also fits into a picture where the wave velocity is proportional to the reciprocal of the square root of the density of the medium, as with sound waves. It is postulated that the density of dark matter outside the sun is proportional to the reciprocal of the distance from the sun's center squared. Evidence for the hypothesis is presented, a wave equation confirms the hypothesis, and implications are discussed.

KEY WORDS. Dark matter, standing waves, solar cycle, planets, sun, satellites, universe, solar system, inertia.

1. INTRODUCTION

Presently there is an extensive search going on to identify dark matter. Is it composed of WIMPS, or hot or cold dark matter, or ordinary matter which cannot be seen readily, or is it something else? I quote Scott Tremaine in Physics Today: "At present we must admit with some embarrassment that we don't know what most of the universe is made of"¹.

It is proposed that the properties of dark matter may shed light on the following outstanding problems in physics. I quote or summarize from Physics Today articles:

1. "The long term stability of the solar system is one of the oldest unsolved problems in physics"².
2. "A fully self consistent model for the "solar cycle" is still being sought"².
3. Life in the solar system "developed to a degree of sophistication that seemingly defies the second law of thermodynamics"³.
4. The present model for the formation of the solar system remains largely theoretical rather than directly applicable without an explanation for its long term stability^2,3.

The above material suggests that a model that explains more about the complex organization and provides for long term stability of the solar system (as well as the universe) and some of the unique aspects of life would be welcome. For the past 11 years I have been publishing data and theory on unique slow moving waves that I first identified in 1988. Perhaps these waves provide important answers to some of the problems of the solar system and the universe that have not been satisfactorily explained. What I am about to present appears to complement rather than supplant the known mechanisms for solar system development and organization.

2. EARLY DEVELOPMENTS

In 1988 I first reported finding slow moving longitudinal waves in plants (velocities near 1 m/s), in ion filled porous materials, and in the space surrounding these materials^4-13. I called the waves W-waves because they were first found in live wood. Standing waves in solid matter appeared to move charge something like sound moves dust in a Kundt's tube. The variations in charge density were indicated by periodic potential differences as high as one volt. Since charge is one of the few things free to move in solid matter this was considered more of a mechanical rather than an electrical effect but this permits observation of wave effects in some solids. The vertical and horizontal wave velocities in plants appear to be different providing a reference for the gravitropism of plants and perhaps indicating a cosmological connection. The special time of flight methods used to measure W-wave velocities are described in a book published in 1995 (p.19) and in a later paper^9,13. I published experimental results, demonstrating that these waves exist, from analysis of charge organization and other features in both plants and ion filled porous materials. The experiments indicate that the reported waves appear to be an all pervading major organizing factor for plants, perhaps all life, and perhaps the solar system as well.

Materials and plants were placed in closed heavy gauge aluminum shields (and in a mine 300 m underground) with probes to monitor voltages. The probe output was fed to low noise, high gain, battery operated amplifiers contained within the shields and the amplifier outputs were monitored on an external low frequency spectrum analyzer. The typical plant spectra observed contained the most usually observed above ground spectra with integral multiples of 1.6 Hz (as well as other typical harmonic series like integral multiples of 0.6 & 2.666.. Hz). It is unknown, as yet, what produces these unique frequencies which I designate eigen frequencies.

The same dominant frequencies were also found by measuring many thousands of typical spacings between adjacent plant structures (internodal spacings). These spacings were assumed to be half wavelengths of standing wave patterns. The spacings were then converted to frequency by using experimentally determined wave velocities. Distributions were taken which demonstrated that plant spacings are quantized with the same unique frequencies apparent as measured with the spectrum analyzer. Vertical velocities were found to be usually larger than horizontal velocities in plant material which apparently provides a reference for the plant's response to gravity. Ratios of vertical to horizontal velocities were confirmed by comparing averages derived from plant internodal spacings^12,13 as well as by direct measurement.

Recent experiments seem to suggest that electromagnetic sources excite a unique set of slow moving wave modes in the surrounding medium. W-waves may be produced by electromagnetic interaction with the dark matter-vacuum medium which may include ordinary matter. Excited W-wave frequencies apparently are characterized more by the medium rather than the electromagnetic source. Some forms of matter such as live plants appear to be wave guides for W-waves. The modes excited electromagnetically seem to be largely independent of the electromagnetic exciting frequency. 60 Hz, 26 khz, 400 khz, 1270 khz, and other sources have been tested at this laboratory. W-waves also are likely excited by other forms of energy such as those found in the sun.

Some have suggested that one might describe W-waves by Maxwell's equations. Maxwell's equations resulted from the observation of the macroscopic behavior of pure electromagnetic waves and probably would not apply to W-waves. It is the author's opinion that Maxwell's equations do not represent ultimate fundamental physics but only what humans have observed so far. I place W-waves in a class with inertia which arises from the vacuum and humans generally only speculate about. The vacuum characteristics are also probably relevant to W-waves so I talk about the dark matter-vacuum medium. There seems to be quantum like behavior associated with W-waves.

It was found that the distributions of plant internodal spacings seem to be different when grown in the presence of certain magnitudes of 60 Hz electromagnetic fields arising from an electric power substation (See chapter nine of the book Waves in Dark Matter⁹). A semiconductor detector, in the vicinity of electronic equipment operated at 60 Hz, driving a low frequency spectrum analyzer usually indicates a large amplitude presence of typical eigen frequencies including 26.7 Hz and 80 Hz for example. These frequencies as well as 60 and 120 Hz are also found in the spacing spectra of plants (derived from plant internodal spacings) far away from 60 Hz sources and in fossil plants. The latter peaks are usually of small amplitude (the author analyzed thousands of spacings from fossil plants in the fall of 1989. Most of this work remains unpublished.)

If one floats materials (like styrofoam particles or plastic beads) on water in the presence of electromagnetic sources it appears that the floatant tends to collect in concentric equally spaced circles (at nodes apparently) around an approximately cylindrical source like an operating vacuum tube. A 6L6 vacuum tube oscillating at 400 Khz at about 30 watts produced 9 cm spaced circles. 9 cm is the half wavelength for 26.7 Hz suggesting that the waves causing the effect are traveling in air at 480 cm/s as was found earlier⁵. Is it possible that the waves travel, perhaps in some cases, at the same velocity in both air and water since later experiments suggest that multiple velocities are possible¹³?

Different sources produce somewhat different dominant wavelengths. It was possible to find similar spacings, with an air medium, using a semiconductor detector attached to an optical table moving toward or away from a vacuum tube source. A mechanical method also showed that the circles seemed to be produced by forces pushing from both directions to keep an instrument on location.

3. EFFECTS OF W-WAVES ON SPACE

Experiments like the latter may indicate that energy is being absorbed from electromagnetic waves to produce the observed effects in the surrounding space. The produced wavelengths, frequencies, and velocity are much different than the corresponding quantities for the producing sources. The resultant wavelengths, frequencies, and velocity correspond to similar quantities in plants. The experiments mentioned could lead to tests proving that the cosmic red shift is due to photon energy degradation rather than the big bang.

I now assume that many bodies, if not all, in the universe oscillate with the slow moving waves discussed. I assume W-waves from an oscillating sun penetrate everything in the solar system and the absorbed energy oscillates in everything. Dark matter and the vacuum may be the basic medium permeating every material object and "empty space". Ordinary matter seems to have large effects on the W-waves traveling through it.

Directly observable wave effects are seen on Saturn. When Voyager took photographs of the North pole of Saturn a hexagonal pattern in a jet indicates standing waves. Calculations suggest that the frequency involved is a harmonic of a fundamental oscillating frequency of the planet. The stability of the zonal jets on Jupiter and Saturn may also be partly due to standing wave effects¹⁴ from oscillating slow moving modes of the planet and its surface.

Physicists on both the West and East coast have found charge organization in materials such as rocks (petro-voltages) in constant environment shielded containers but left the data unpublished (except for internal reports which I obtained) because of the lack of a theory. Often coincident pulses or other unique coincident wave forms were outputted simultaneously from shielded materials at different locations. It is well known that plant rhythms don't change whether they are growing on the earth's surface or deep underground under a steady light. If plants are operated by waves, as I find, then these waves penetrate matter everywhere. All the findings thus far seem to indicate all pervading wave action. I reasoned that the solar cycle might be produced by oscillations of similar waves^9,10. If the solar cycle is produced by this species of waves, then they also are also very slow moving waves in the sun's matter (near 1 m/s) as found in plants and elsewhere.

It may be that many objects in the universe oscillating with these slow moving waves are surrounded with standing waves that in the case of the solar system, for example, had something to do with the placement of the planets and the satellites and rings of the planets. A simple equation was found by linear regression and experiment that describes the placement of the planets^9,10:

(1)

where r is the distance from the center of the sun, r₀ is the sun's effective radius (which depends on a star's composition when the satellites are placed). N is an integer for a particular planet. Notice that equation (1) can also be written as 1.6pln(r/r₀)=Np. Using a 5 % larger radius then the present sun's radius for r₀ (7.3 x 105 km) and N=7 and 8 give the radii of Mercury and Venus's orbits almost exactly, and Neptune's orbit (N=14), within 2.4 %, considering that they had circular orbits initially. Probably collisions and other disturbances changed most of the orbits from circular to elliptical while they were forming or afterward. All the other planet orbital radii including that for Ceres (using mean value circular orbits) then fit within 14 percent or better (except for Pluto and Earth) using N= 9, 10, 11, 12, 13, 14, and 15. The locations of satellites of planets are also described very well by this equation with proper choices for r₀^9,10 (see Tables I, II, and III and the discussion section and other publications⁹ for reasons for variations). Others have found more complex equations that work for the sun's planets but none that work for satellites of planets (from unpublished work). The idea that equation (1) is so simple makes it attractive.

4. A WAVE EQUATION

If equation (1) holds it implies that the velocity of the proposed waves increases as they move away from the sun. The following velocity equation is suggested by equation (1):

(2)

where v is the velocity and v₀ is a constant (on the sun the radial W-wave velocity at the surface). The type of behavior hypothesized here suggests that longitudinal waves are involved and that perhaps standing waves are produced by reflections due to density and velocity gradients, for example. There is the possibility that the observed phenomena could be due to some other minimum energy phenomena that is not recognized yet.

Several equations follow from equations (1) and (2). For example if equations (1) and (2) are correct one can solve for N from (1) and substitute it into (2) with the result that:

(3)

This simple result can now be substituted for v in the following simple wave equation:

Equation (1) gives the location of nodes (at r=r₀ or greater) so it follows that the locations are also described by sin(1.6pln(r/r₀)) with the zeros of the function located on nodes. The latter suggests a standing wave like solution for (4). We now assume a solution for (4)(using spherical co-ordinates) of the form F=F₀f(r)e^iwt and substitute it into (4) with w=w₀. The resultant differential equation is then solved for f(r). A solution is f(r)=C₁r^-1/2 sin(r₀w₀/v₀ ln r/r0) for r>r₀. C₁ is a constant. f(r) has been simplified somewhat from the original solution (see the appendix). Notice that if r₀w₀/v₀ is equated to 1.6p (from above; note that 1/0.625=1.6), v₀ comes out to be 1.25 m/s using the mean solar cycle period to determine w₀. In the past I have usually used approximately 1 m/s as the mean velocity of W-waves traveling radially in the sun. The 1.25 m/s is also calculated using an integration in another source on page 91⁹.

Since oscillating bodies are being considered it seems appropriate to think of r₀ as a wavelength or half wavelength. The average velocity of the waves in planets is assumed to be approximately proportional to the reciprocal of the square root of the planet's mean density. Equation (1) is assumed to hold when satellites or planets are placed. Subsequent changes in radius may have occurred with large temperature changes, with added mass, etc. Satellites may have been added as mass was being added to a planet. Several possible scenarios are discussed elsewhwere⁹. If a planet or star vary in mean density the wave medium outside the planet or star would also vary similarly in density because of the different total masses. For a given diameter a less dense planet would oscillate at a higher frequency than a more dense planet. Less dense bodies (for example Saturn is less dense than Jupiter) hold less of the surrounding dark matter medium with a resulting larger velocity for the waves traveling within and to and from the body. Thus equation (1) holds for both Jupiter and Saturn but Saturn is about one half as dense as Jupiter. The satellite locations seem to indicate that both Jupiter and Saturn were close to the same radius (approx. 80,000 km) when they were very hot and most of their satellites were placed⁹.

An approximate expression for the frequency of oscillation of the sun and other bodies apparently is: 1.19/(r₀Öd) where d is the relative mean density (with water as 1.0) (note that the sun's radius in meters is just equal in magnitude to 22.2 years (the apparent solar cycle period) in seconds). 1.19 is the square root of the sun's mean density. I applied this expression to about 50 main sequence stars, using actual radii for r₀, with considerable variation in radius and relative mean density. The resulting values were nearly the same for the oscillation frequencies of all the stars used in the calculations. Two departures from the same value may be explainable in terms of changes in the wave velocity function as a function of star density. Note that others have used the reciprocal of the square root of the mean density in discussing variable star oscillations¹⁵. The relative mean density of the sun is 1.41, of Jupiter 1.33, and of Saturn 0.69.

5. DARK MATTER DENSITY FUNCTION

If one assumes that the hypothesized waves behave like sound waves in ordinary matter then the velocity of the waves varies inversely as the square root of the density of the medium. Setting equation (2) equal to the reciprocal of the square root of the density (multiplied by a constant and using N=1.6 ln r/r₀ from equation (1)) yields the following for the density function:

(5)

where d is the density and C is a constant. The density of dark matter in the solar system apparently is so small that it doesn't appear to have any consequence as far as most classical physics is concerned but again we may be dealing with something perhaps as elusive as inertia, for example, which is a very large effect.

The density function (equation (5)) is just the density function one can derive simply or others have reported for dark matter around galaxies(for r much larger than r₀). This is concluded because outer stars move at constant velocity in orbits about the centers of galaxies. The density of dark matter, in the outer periphery of the Milky Way, for example, apparently varies as the reciprocal of the square of the distance from the galactic center for large r₀^1,16. It should be pointed out that the actual distribution of dark matter around the sun is unknown. Equation (1) may not hold for very large N and r but I would still expect W-wave velocities to become very large far away from ordinary matter.

6. DISCUSSION

In the past Bode's law has been found useful in locating the planets (see astronomy and elementary physics texts). For Bode's law the series 0, 3, 6, 12, 24, 48, 96, 192, 384, and 768 is used to initiate the calculation. Next 4 is added to the numbers giving 4, 7, 10, 16, 28, 52, 100, 196, 388, and 772. If earth's distance from the sun is 1 AU this can be used for the 10 in the series. Then Mercury is at 3.8, Venus 7.2, Earth 10, Mars 15.2, Ceres is at 27, Jupiter is at 52, Saturn is at 95.5, Uranus is at 192, Neptune is at 301, and Pluto is at 396 (note that equation (1) does much better than Bode's law for Mercury, Venus, Neptune, and Pluto). One can see that there is a reasonable fit in Bode's formula for the first 8 planets. Bode's empirical recipe was found to work reasonably for these planets but the results lead nowhere because no theory is suggested. The formula helped locate outer planets early in the development of astronomy, however. Bode's law suggests a rapidly increasing velocity wave function as the waves get farther from the sun if waves are involved in planet placement.

Equation (1) not only works well to locate the planets, taking into account early circumstellar matter⁹ which would tend to decrease the wave velocity, but it works well to locate the satellites of gaseous planets as well (e.g. see Tables I, II, and III). We do not know the initial conditions when the satellites of planets were positioned but if equation (1) is correct a reasonable early solar system history results⁹. Equation (1) does not describe the locations of all the sun's planets exactly perhaps because matter was distributed around the solar system in a different manner when the satellites and planets were placed. There probably was much circumstellar ordinary matter still present.

Non-uniformly distributed matter (including dark matter) would have a large effect on planet placement in a wave operated system. Equation (1) does describe the locations of Mercury and Venus exactly because the solar wind had cleared the region of the less dense matter when they were placed. Wave amplitudes would also be larger closer to the sun source because of the spread of the waves through an area increasing as r². The author of reference 3 suggests that the accretion of volatiles on the giant planets implies that they must have formed before the solar nebula was completely dissipated³. The presence of excess matter (increased density regions departing from the distribution assumed by equation (1)) in space would tend to decrease the wave velocity thus producing closer spacings. For example Mars and Earth may have been gaseous planets in a residual circumstellar matter ring or disk whose density varied with distance from the sun. One would expect the intermediate planets to be affected most by primordial excess circumstellar matter because such matter would most likely be located in their vicinity.

The special initial conditions permitted the formation of what now appears to be an extra planet from equation (1), the earth (of course there is also the possibility of a planet being injected into the system). When the circumstellar matter between the planets finally dissipated it left Earth and Mars more or less where they are today with other planets not fitting equation (1) exactly (see Table I). I would still expect the system to be stable, however, because the ever present standing wave pattern would tend to stabilize the system.

One cannot say at this time what the early matter distribution was. Assume an early effective radius (r₀ of 7.30 x 10⁵ km since this seems to produce a rather good fit taking into account excess matter during placement.

• Sun's Radius: 695,893 km
• Orbit equation:r=r₀(exp(0.625N))

Table I. A comparison of the actual distances r of the planets from the sun's center with the calculated distances using the orbit equation given above. N is an integer. Note that the middle planets don't fit as well as the inner or outer planets as one might expect if one takes into account the extra circumstellar matter that was present when the planets were placed. Circumstellar matter would tend to reduce the wave velocity and thus change the planet spacings (see the text).

Table II. A comparison of the actual distances (r) of the satellites of Jupiter from the planet center with the derived distance using the orbit equation above. Again, as with the sun, excess matter (and other factors such as collisions) present when the satellites were placed likely caused differences. It is likely that Jupiter was larger when the outer satellites were placed but wave effects tended to keep the closest satellites in wave orbits as the size decreased (or the inner satellites were placed after the planet cooled). Thus I show placement using both the present radius and a larger effective radius for the outer orbits (see the text).

Table III. A comparison of the actual distances of the satellites of Saturn from Saturn's center with distances calculated using the orbit equation given. Note that there are small differences but the presence of other matter and catastrophic events such as collisions over the course of a long time would be expected to make differences. Otherwise it appears there is an obvious correlation. Notice the missing satellite at 3559 km for Jupiter. The corresponding satellite (Iapetus) is present for Saturn. This is additional evidence the proposed wave theory is correct.

In considering tables I, II, and III, in the wave theory, one would expect the satellites or planets closest to the planet or sun to fit equation (1) the best due to the large amplitude of the waves closest to the source (or oscillator). I thus chose the effective radius (r₀) to fit this condition. According to Table I the apparent effective radius of the sun (taking into account the wave velocity within the oscillating body) appears to be close to 7.30 x 10⁵ km. This radius is slightly larger than the present radius as might be expected. The first two planets fit almost exactly even though the first one is at N=7. Anything located at an N smaller than 7 would apparently have been blown away by the solar wind.

In Table II, for Jupiter, the first 3 satellites don't fit well with the large radius apparently because the radius was considerably larger because of the planet's high temperature when the outer satellites were placed. If one uses the present radius the first three satellites fit well which is consistent with the idea that these satellites were placed after the planet had cooled down. Another possible explanation that fits in with the wave hypothesis is that the closer three satellites tended to be forced in closer to fit the proper orbits as the planet cooled because the amplitude of the wave action is larger closer to the planet.

In table III, for Saturn, the effective radius that I chose by trial and error seems to work well for most of the satellites. The effective radius chosen suggests Saturn was also very hot when its satellites were placed and considerably larger as one would expect for a gaseous planet. Notice in table 2 for Jupiter there is a satellite missing at 3559 kilometers. The corresponding satellite is present for Saturn (Iapetus). The ideas here again suggest that the wave hypothesis is correct.

7. CONCLUSIONS, OBSERVATIONS, AND IMPLICATIONS

Some of the possible implications, ramifications, and results of the above simple calculations, experiment, and discussion include:

1. Dark matter in the solar system may be vibrating at large amplitudes, from the sun's energy, at the solar cycle frequency (as well as other frequencies). A study of the orbits of natural satellites indicates quantization due to wave action (Tables I, II, and III). If the waves travel at high velocities in very low density dark matter (see equations 2 & 3) they could explain periodically spaced "Great Walls" and other large structures in the universe^17,18. The universe would probably need to be older than presently considered to permit such large structures to develop under relatively low velocity wave action, if it took many cycles to form these structures.
2. Dark matter pervades everything and is not just dark chunks of ordinary matter located where they can't be seen. The wave hypothesis favors an energetic dark matter model which provides for much of the observed lumpiness of the universe¹⁸.
3. Dark matter-vacuum waves may provide continuous stabilization for the solar system with ordinary matter perhaps collecting at nodes during planet formation according to equation (1). Standing waves may always be present due to excitation by the sun. The sun's oscillation, with the resultant radiation into the space around it, is presently indicated by the solar cycle. Thus continuous stabilization and organization is provided.
4. A reasonable history of the solar system appears to result from the work here^9,10. The sun, Jupiter, and Saturn all manifest a similar behavior in satellite placement. It makes sense that the placement function was a function of something that increased in velocity as it got farther away because of the nature of the satellite spacings in all three cases.
5. The interactions of these waves, in earthly materials, with electromagnetic phenomena appear to be small. For example effects on plants by electromagnetic waves are subtle. This might be expected if the waves observed in earthly materials are also waves in dark matter as I have hypothesized.
6. Plants may collect and concentrate the wave medium. The special spectra from the salt solution filled materials mentioned in the introduction may at times show amplitudes at most an order of magnitude above the noise. In plants, however, the amplitudes may be an order of magnitude higher yet. Experimental indications are that the waves develop large amplitudes in plants⁸.
7. Dark matter present in the sun may explain the solar neutrino problem because it cools the sun's interior¹⁶. W-waves may absorb energy.
8. Recent experimental results in plants indicate that the waves travel at different velocities depending on whether they are traveling parallel or perpendicular to the gravitational field. This may explain how plants interact with gravity (gravitropism) and suggest important implications for cosmology 9,10,12,13. For example in the book (Waves in Dark Matter)⁹ it is suggested that the location of a planet is initially determined by a double node. One node is in standing waves that circle a star perpendicular to the gravitational field. The other one is in the standing waves that radiate radially from it along the gravitational field. A planet (or satellite) forms where the nodes intersect. This puts special requirements on the relationship of velocities of in-phase waves perpendicular and parallel to the gravitational field in space. The nature of the node (whether single or double) determines whether a ring or satellite is formed around a planet. Rings are formed when there are independent radial nodes produced by non- fundamental oscillations due to reflections from layers within a planet⁹. Ring structure then reflects a planet's internal structure.
9. In the formation of spiral galaxies the centrally located structure may have produced pairs of jets that injected matter into resonant orbits. Initially the central structure was larger and thus r₀ was large. As the central structure lost mass r₀ became smaller and the radius of the resonant orbit smaller. Rotation of the forming spirals, for proto spiral galaxies, with possible drag in dark matter, may be essential in the spiral forming process. I am assuming trailing spiral arms¹⁹. In general the direction of the angular momentum of the central structure relative to the accompanying structure may determine the type of galaxy formed. Note that density waves in ordinary matter are considered essential for galaxy formation by others. I have added density waves in dark matter.
10. Since the experiments and observations on earth seem to indicate quantization, I wouldn't be surprised that star sizes with their masses are also quantized so that if a star is too large for a proper oscillation frequency, for example, it tends to throw off the excess matter.
11. These waves may imply that dark matter is a large energy sink. Much of the energy might come from light and perhaps change our present view of the expanding universe. My experiments with electromagnetic sources that seemed to produce slow moving waves may indicate that dark matter absorbs energy from electromagnetic waves. If so does this absorption degrade photon energy? Experiments need to be devised to check this out. A comparable energy degradation may produce the cosmic red shift. Thus in large concentrations of dark matter one might find relatively large red shifts. Perhaps quasars are "exploding" huge concentrations of matter with an accompanying large concentration of dark matter. One might find a relatively large red shift in such a dense dark matter situation if my hypotheses are correct. Also dense dark matter might absorb kinetic energy as it flows through passing matter. The apparent kinetic energy decay of objects orbiting pulsars could thus be attributable to energy absorption by dark matter.
12. These waves may explain other anomalous phenomena on earth. For example Fibonacci numbers (or the Golden ratio) found in plant structures and elsewhere²⁰. Quasicrystals may suggest the common action of the all pervading waves discussed here⁶.

8. OTHER IMPLICATIONS AND SUMMARY

We may not understand completely how these waves are related to the gravitational constant but these waves manifest themselves in many different ways in the solar system as discussed. These include in the spacings of the moons and planets and in the rings of the planets. These waves may be a decisive force in determining the stability of the solar systems. These waves are just as important today as in the past, however, planetary collisions with other objects, for example, have obscured some of the basic results of the fundamental wave action.

The wave hypothesis that I have presented may solve a multitude of problems for the universe as a whole. It may provide an answer as to why the universe is apparently excessively lumpy for the present extant theory to explain properly. Large bubbles may exist in space because large amplitude oscillations in dark matter have forced baryonic matter to the periphery. Oscillations at high frequencies may produce the high temperatures observed in gas clouds, and may have something to do with the x-ray background. The wave hypothesis appears to provide a simple solution as to why rings of gaseous planets don't appear to dissipate (continuous stabilization) even without shepherd moons present and why sometimes there is a ring rather than a satellite. Perhaps the ring structure of a gaseous planet mirrors the internal structure of the planet etc.^9,10. I believe, because the wave solutions are so simple compared to other proposed solutions, that the wave hypothesis provides a very viable alternative to other hypotheses. Additionally it provides continuous solar system stabilization which a correct theory would need to provide. The simple solutions and stabilization that the wave hypothesis provides are strong arguments in favor of waves in the dark matter-vacuum medium providing organization and stabilization for the solar system. Otherwise chaos would probably have destroyed the solar system long ago (or it should have never developed) as has been calculated using chaos theory²¹.

APPENDIX: MORE ON THE SOLUTION OF EQUATION (4):

The differential equation in r resulting from substituting the proposed solution F=F₀f(r)e^iw0^t into the wave equation in spherical co-ordinates is r²f"(r)+2rf'(r)+C₂f(r)=0. C₂ is a constant and equals (r₀w₀/v₀)^2.. The given differential equation is a common differential equation with complex roots here. A general solution is:

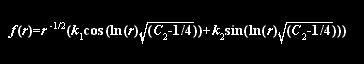
where k₁ and k₂ are constants. The sine and cosine solutions are discussed, for example, on pages 259 and 260 of "Elementary Differential Equations and Boundary Value Problems" by Boyce and DiPrima, Wiley 1996, 6th ed. To evaluate C₂ use the period (T₀) of the solar cycle as the number of seconds in 22.2 years and the fact that r₀, the radius of the sun in meters, is equal in magnitude to 22.2 years in seconds (remember that w₀=2p/T₀). This leaves (2p)² in the numerator of C₂ and using v₀ as approximately 1 m/s gives C₂=39.5 thus C₂>>1/4 under the square root. Neglecting the 1/4 results in about a 0.3 % error in the square root. ln (r/r₀) is substituted for ln r because ln (r/r₀) can be written as (ln r -ln r₀) with ln r₀ a constant not affecting the validity of the solution. These considerations together with known data produce the simplified solution to the wave equation in the text with the r part of the solution given by: f(r)=C₁r^-1/2sin(r₀w₀/v₀ ln r/r₀).

ACKNOWLEDGMENTS

I wish to thank Dr. Robert Zimmermann of the University of Oregon physics department for the long discussions we had on the subject of waves in dark matter. I also wish to thank Dr. Kemble Yates and Dr. Art Clemons of the Southern Oregon University mathematics department for their suggestions. I thank Eric Moret of the Oregon State University physics department and the Southern Oregon University foreign language department for translating the abstract into French. I am grateful to my wife Claudia for reading and checking the manuscript.

REFERENCES

1. S. Tremaine, Phys. Today 45, 28-36 (1992).
2. C.F. McKee and W.H. Press, Phys. Today 44, 69-73 (1991).
3. A.I. Sargent and S.V.W. Beckwith, Phys. Today. 46, 22-29 (1993).
4. O.E. Wagner, Northw. Sci. 62, 263-270 (1988).
5. O.E. Wagner, Northw. Sci. 63, 119-128 (1989).
6. O.E. Wagner, Northw. Sci. 64, 28-38 (1990).
7. O.E. Wagner, Physiol. Chem. Phys. and Med. NMR 24, 29-34 (1992).
8. O.E. Wagner, Physiol. Chem. Phys. and Med. NMR 25, 49-54 (1993).
9. O.E. Wagner, Waves in Dark Matter (Wagner Physics Publishing, Rogue River, OR, 1995) (available from the publisher).
10. O.E. Wagner, Bull. Am. Phys. Soc. 36, 1320 (1991).
11. O.E. Wagner, Physiol. Chem. Phys. and Med. NMR 27, 31(1995).
12. O.E. Wagner, Bull. Am. Phys. Soc. 39, 1809 (1994).
13. O.E. Wagner, Physiol. Chem. Phys. and Med. NMR 28, 173-196 (1996).
14. J. Kelly Beatty and Andrew Chaikin, The New Solar System (Sky Publishing Corporation, 1990) pp. 146,147.
15. K.R. Lang, Astrophysical Formulae (Springer-Verlag, 1980), p.537.
16. L.M. Krause, The Fifth Essence (The Search for Dark Matter in the Universe), (Basic Books Inc. 1989) pp. 61-70, 290, 291.
17. T.J. Broadhurst, R.S. Ellis, D.C. Koo, and A.S. Szalay, Nature 343, 726-728 (1990).
18. Faye Flam, Science 254, 1106-1108 (1991).
19. J. Binney and S. Tremaine, Galactic Dynamics, (Princeton University Press, 1987) pp 343-345.
20. R. Dixon, Computers Math. Appl. 17, 535-538 (1989).
21. Ivars Peterson, Sci. News 141, 120-121 (1992).